Über Mathematik im Bilde sein

Bilder und Videos sind aus dem Internet nicht wegzudenken. 2022 wurden zum Beispiel in jeder Minute durchschnittlich 64.440 Fotos oder Videos auf Instagram geteilt und 167 Millionen Videos auf TikTok angesehen.

Dank immer besserer Smartphone-Kameras haben digitale Filme und Fotos einen festen Platz im Alltag Jugendlicher. Kaum eine Situation bleibt fotografisch undokumentiert, Bildbearbeitung und Filmschnitt per App sind buchstäblich ein Kinderspiel.

Weniger verbreitet ist das Wissen um die mathematischen Hintergründe digitaler Bilder und Videos – dabei ist es für junge Fotograf*innen ziemlich nützlich, Begriffe wie Auflösung, Farbtiefe oder Bildrate zu verstehen. In diesem Lehrerspezial schlagen wir deshalb den Bogen von digitalen Bildern zum Mathematikunterricht. In den Unterrichtsideen lernen Schüler*innen zum Beispiel Pixel und Auflösungen kennen, beschäftigen sich mit verschiedenen Kompressionsverfahren, filmen per Stop-Motion-Verfahren einen Ballwurf und erstellen aus Vektoren Kunstwerke.

Die Welt in Pixeln

In der Vorstellung vieler Menschen sind Pixel kleine Quadrate, die sich zu größeren Bildern zusammenfügen. In Wirklichkeit sind Pixel nicht zwangsläufig quadratisch und es besteht auch nicht jedes Bild aus Pixeln. Zutreffend ist aber, dass digitale Bilder und Rastergrafiken aus einzelnen Bildpunkten bestehen, die so klein sind, dass das Auge im Idealfall keine einzelnen Elemente wahrnimmt, sondern durchgehende Linien und Flächen. Wie groß ein Pixel ist, hängt von der Auflösung eines Bildes oder Bildschirms ab: Je mehr Pixel sich die verfügbare Fläche teilen, desto kleiner ist jedes einzelne. Wer die Mathematik digitaler Bild- und Filmwelten verstehen möchte, findet mit Pixeln einen guten Einstieg.

Grafiken, die bei Vergrößerung nicht verpixeln

Etwas künstlerischer lässt sich die Beschäftigung mit Bézierkurven gestalten, indem die Schüler*innen zum Beispiel eigene Logos oder Buchstaben entwerfen. Sie lernen dabei, dass nicht jedes Bild aus Pixeln besteht. Buchstaben etwa werden nicht pixelig, wenn am Computer die Zeichengröße erhöht wird. Der Grund: Schriften, ebenso wie viele Logos, sind nicht als Bilder angelegt, sondern werden mathematisch beschrieben als sogenannte Vektorgrafiken. Ein beliebtes Hilfsmittel dafür sind Bézierkurven, bekannt nach dem Ingenieur Pierre Bézier, der in den 1960er Jahren Auto-Karosserieformen entwickelte.

Heute begegnen viele Menschen Bézierkurven zum ersten Mal in Software wie Microsoft Powerpoint: gekrümmte Linien zwischen zwei Punkten, die Krümmung lässt sich beeinflussen, indem man zwei weitere Punkte verschiebt. Mehrere Bézierkurven lassen sich zu beliebigen Formen zusammensetzen und dann ohne Qualitätsverlust vergrößern.

Algorithmen: Filme und Bilder komprimieren

Digitale Bilder und Filme benötigen viel Speicherplatz. Das ist unpraktisch, wenn man sie schnell versenden möchte. Gut, dass man bei Bedarf die Dateigröße reduzieren kann – je nach Kompressionsmethoden mit oder ohne Verlust. Für den Mathematik- oder Informatikunterricht bieten Kompressionsverfahren interessante Einblicke, um besser zu verstehen, wie Mathematik Alltagsprobleme lösen kann. Konkret lässt sich außerdem die Funktionsweise von Algorithmen vermitteln.

Verlustfrei komprimieren: Lauflängen- und Huffman-Kodierung

Wie lässt sich digital Platz sparen? Die Frage birgt nicht nur eine mathematische, sondern auch eine kreative Herausforderung. In der IT gibt es verschiedene Lösungsansätze.

Zu den offensichtlichsten Vorschlägen gehört eine so genannte Lauflängenkodierung, auf Englisch „Run-Length-Encoding“ (RLE) genannt. Die Idee ist einfach: Anstatt Informationen über jedes einzelne Pixel zu speichern, fasst die Lauflängenkodierung nebeneinander liegende, identische Pixel zusammen. Wie das genau funktioniert, erklärt dieses Video . Vereinfacht gesagt wird dadurch aus

Das Beispiel lässt bereits ahnen, dass sich Bilder unterschiedlich gut per Lauflängenkodierung komprimieren lassen: Je weniger Farben ein Bild umfasst und je großflächiger die Farben verteilt sind, desto stärker lässt sich durch die Lauflängenkodierung die Dateigröße verringern.

Ein auch für komplexere Dateien geeignetes Verfahren ist die Huffman-Kodierung . Sie kodiert jedes Zeichen einzeln, aber häufige Zeichen bekommen eine besonders kurze Kodierung. Wie der Algorithmus funktioniert, lässt sich mithilfe von Baumdiagrammen demonstrieren.

Lernen wie im Flug: Eine Seilkamera bauen und mathematisch erkunden

Wenn es – zum Beispiel im Fußballstadion – auf großer Fläche viele Aktivitäten und spannende Details zu sehen gibt, hilft eine Seilkamera weiter. Sie hängt an vier Seilen, die hoch oben aus den vier Ecken über der zu filmenden Fläche zur Kamera führen. Über Seilwinden lässt sich die Position der Kamera im dreidimensionalen Raum verändern, so dass sie immer dort filmen kann, wo es gerade besonders viel zu sehen gibt. Seilkameras sind nicht nur nützlich, sondern bieten im Mathematikunterricht auch einen interessanten Einstieg in die analytische Geometrie.

Wie die Schüler*innen mit einfachen Mitteln in Gruppenarbeit selbst Seilkameras bauen und sich in sieben Stationen die Grundbegriffe der analytischen Geometrie praktisch erarbeiten, erklärt ein Unterrichtsmaterial des Sinus-Projekts in Nordrhein-Westfalen .

Noch spannender wird es, wenn die Seilwinden nicht menschen- sondern computergesteuert funktionieren und per Python oder Scratch von den Schüler*innen selbst programmiert werden.

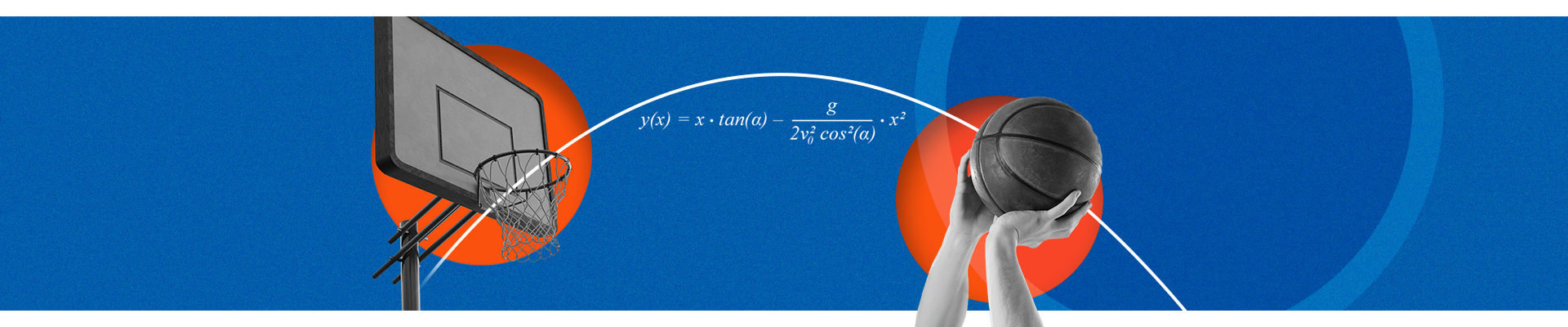
Stop-Motion-Animation eines Ballwurfs per Stop-Motion

Wie viele Bilder pro Sekunde sind nötig, um den Eindruck einer flüssigen Bewegung zu erzeugen? Das ist die Kernfrage, der die Schüler*innen in dieser Stop-Motion-Aufgabe nachgehen. Ganz nebenbei lassen sich zudem Parabeln wiederholen. Die Idee: Die Jugendlichen stellen auf Papier einen Ballwurf nach und filmen ihn möglichst flüssig im Stop-Motion-Verfahren. Ein echter Ball ist dabei nicht nötig, die ganze Animation spielt sich auf einem DIN-A4-Blatt ab. Der Ball – bzw. ein ausgeschnittener Kreis – soll in einer realistischen Kurve von links nach rechts fliegen und dort einen Korb treffen. Die Aufgaben umfasst fünf Schritte.