Mathematische Sachverhalte...

Nach dem wir unsere Fundstücke gesichtet haben, sind wir dazu übergegangen die mathematischen Sachverhalte zu klären. Hier sehen Sie, was wir an mathe-matischen Sachverhalten entdeckt haben.

 

Symmetrie

Mit dem geometrischen Begriff Symmetrie bezeichnet man folgende Eigenschaft: ein geometrisches Objekt kann durch bestimmte Umwandlungen auf sich selbst abgebildet werden kann, so dass es unverändert erscheint. Eine Umwandlung, die ein Objekt auf sich selbst abbildet, heißt Symmetrieoperation.
Wir betrachten zuerst die Achsensymmetrie (oder Geradensymmetrie oder Spiegelsymmetrie), die entlang einer Symmetrieachse einen Gegenstand spiegelt.

Dreiecke können eine oder drei Symmetrieachsen haben. Vierecke können eine, zwei oder sogar vier Symmetrieachsen besitzen. Das Quadrat ist Rechteck und Raute zugleich und hat somit vier Symmetrieachsen.
Die Achsensymmetrie tritt im technischen Alltag und in der Natur sehr häufig auf. Bei genauem Hinsehen allerdings ist kaum ein Gegenstand wirklich total symmetrisch.
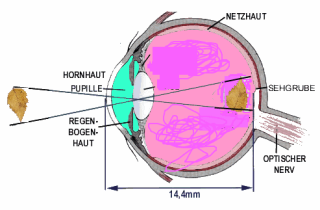
Die Punktsymmetrie ist eine Eigenschaft geometrischer Objekte. Ein geometrisches Objekt heißt punktsymmetrisch, wenn es eine Punktspiegelung gibt, die dieses Objekt auf sich abbildet. Der Punkt, an dem diese Spiegelung erfolgt, wird als Symmetriezentrum bezeichnet. Unser Auge bildet Gegenstände punktsymmetrisch, allerdings stark verkleinert ab. Jedes Bild hätte in Originalgröße keinen Platz auf der Netzhaut. Unser Hirn "macht" dann für uns die Vergrößerung.

 

Stereometrie

Stereometrie oder auch Raumgeometrie ist ein Teilgebiet der Mathematik und befasst sich mit geometrischen Gebilden im Raum. Zur Stereometrie gehört unter anderem die Berechnung der Oberfläche bzw. der Mantelfläche und des Volumens einfacher und zusammengesetzter geometrischer Körper, wie zum Beispiel Zylinder, Kegel, Kugel, Prisma, Pyramide, Tetraeder oder Würfel.

 

Spiralen

Eine Spirale ist eine ebene oder räumliche Kurve, die in bestimmter Weise um eine Mitte läuft. Oder genauer: Eine Spirale ist eine Kurve, die um einen Punkt oder eine Achse verläuft und sich je nach Laufrichtung von diesem/r entfernt oder annähert.

Archimedische Spirale

Die Archimedische Spirale ist eine einfache Spiralen. Sie entsteht, wenn bei einer Drehbewegung der Radius proportional zum Drehwinkel wächst, das heißt es gilt r = a × µ mit Radius r, Drehwinkel µ und a > 0.

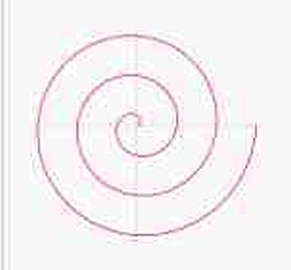
Eine Archimedische Spirale links beginnt im Nullpunkt und beschreibt um ihn eine immer weiter werdende Kurve mit drei Umläufen. Der Abstand der Spiral-Äste bleibt gleich. Genauer: Die Entfernungen benachbarter Kurvenpunkte auf einer Nullpunktsgeraden sind konstant

 

Logarithmische Spirale

Eine logarithmische Spirale ist eine Spirale, die mit jeder Umdrehung den Abstand von ihrem Mittelpunkt um den gleichen Faktor vergrößert. Jede Gerade durch den Mittelpunkt schneidet die logarithmische Spirale stets unter dem gleichen Winkel.

Logarithmische Spiralen besitzen die allgemeine Polar-koordinatenfunktionsgleichung R(x) = a × e^kx.
a ist dabei konstant, also ein beliebiger Vergrößerungsfaktor und k ist eine Konstante, die eine Funktion von x ist.

 

Fibonacci-Spirale

Man zeichnet zuerst zwei kleine Quadrate übereinander. Dann fügt man in Folge immer größer werdende Quadrate entgegengesetzt dem Uhrzeigersinn hinzu. In die Quadrate werden (schwarze) Viertelkreise eingezeichnet. Sie bilden die Fibonacci-Spirale.

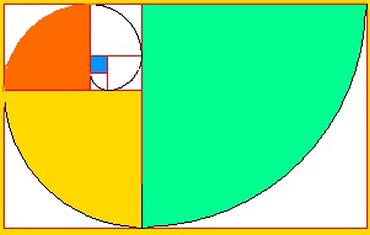
Der Name der Spirale rührt von den Fibonaccizahlen her. Schreibt man die Seitenlängen der Quadrate der Reihe nach auf, so erhält man die Folge 1, 1, 2, 3, 5, 8, 13, 21, ....
Das sind die Fibonacci-Zahlen, die sich nach der Rekursionsformel a(n) = a(n-1) + a(n-2) errechnen [a(1)=1, a(2)=1, n > 2].

 

 

 

 

 

 

 

 

 

 

 

 

 

Viele Pflanzen ordnen ihre Samen von einem Zentrum ausgehend an. Dabei stellt man fest, dass die Anzahl der rechts- und linksdrehenden Spiralen immer zwei aufeinanderfolgende Fibonacci- Zahlen sind.

 

Zylindrische Spiralen

Zeichnet man in ein Achsenkreuz eine Kreislinie mit x = cos(t) und y = sin(t) und zieht sie gleichmäßig in z-Richtung auseinander, so entsteht eine räumliche Spirale. Sie heißt zylindrische Spirale.

 

Flächen in der Natur

Fünfecke

Fünfecke finden wir im Bereich der Pflanzen und in der Tierwelt (Seestern).

 

 

 

 

 

 

 

 

 

 

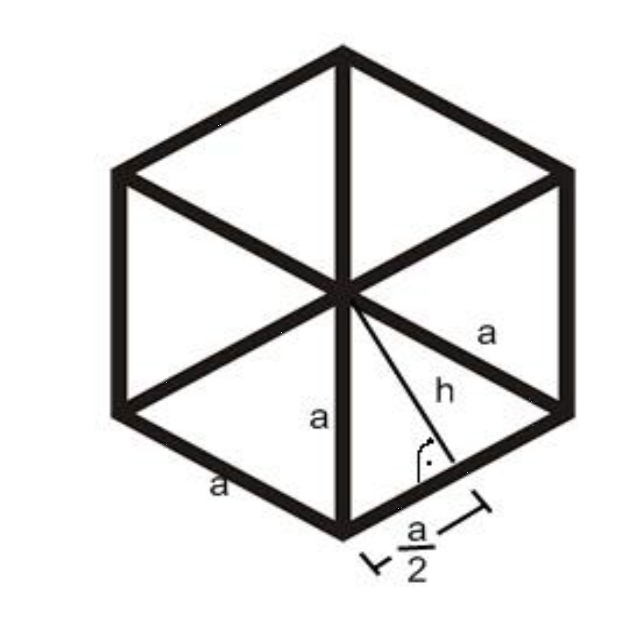
Sechsecke

Jeder kennt sicher das regelmäßige Sechseck in der Natur in Form der Bienenwaben. Auch Schneeflocken haben eine sechseckige Form.