Ist Mathe die Sprache der Natur?

Startseite Mathe in der Natur Musterbildung Unsere Meinung Weiteres

Musterbildung

Von einfachen Zellstrukturen bis zum Aufbau komplexer Zebra-, Leoparden- oder Giraffenmuster. Überall in der Natur können wir das Phänomen der Musterbildung beobachten und gleichzeitig mit der Mathematik versuchen es zu erklären. Doch auf welche Weise entstehen sie? Und können wir diese Muster durch die Mathematik erklären oder sind und bleiben sie eben nur Versuche einer Erklärung? Doch zuerst einmal…

Was sind Muster?
Warum gibt es Muster?
Wie entstehen Muster im Sand?
Der Goldene Schnitt
Die Fibonacci-Folge
Entstehung komplexer Punktmuster

Was sind Muster?

"Unter einem Muster versteht man ein sich wiederholendes, flächenfüllendes Element […]"
Ausschnitt aus einem Artikel von Wikipedia:
de.wikipedia.org/wiki/Muster_(Textil)

"Als Muster bezeichnet man sichtbare Oberflächenzeichnungen oder -strukturen.[…]"
Ausschnitt aus einem Artikel von Wikipedia:
de.wikipedia.org/wiki/Muster_(Struktur)

Das sind zwei Definitionen, die jeweils ein bestimmtes Themengebiet der Muster abdecken! Einmal die Textilproduktion und einmal Musterstrukturen. Anhand dieser Zitate wollen wir selber einen Definitionsversuch wagen:
Als Muster bezeichnet man eine sich auf einem Gegenstand, ein Fläche oder Lebewesen befindende sich wiederholende Struktur, die einen Sinn in ihrem Sein erfüllt, oder einfach gut aussehen soll.

Warum gibt es Muster?

Die Musterbildung auf Tieren bzw. Tierfellen hat im Prinzip nur eine Funktion, die Verbesserung der Lebensbedingungen dieser Tiere. Dazu gehören:
Die Tarnung zum Schutz vor Feinden und zum Heranpirschen an die Beute ist einer der Hauptgründe, wieso Tiere Muster besitzen. Außerdem, und dies gilt nicht nur für Tiere sondern auch für Pflanzen, verdeutlichen bestimmte Farben oder Muster, bestimmte Nachrichten. So meint zum Beispiel Phyllobates terribilis bzw. der "schreckliche Pfeilgiftfrosch" mit seiner Farbe das er äußerst giftig ist.

Wie entstehen Muster im Sand?

Das Beispiel, um die Musterbildung am einfachsten zu verdeutlichen, ist wohl das der Bildung der Sandrippel (kleine Wellen bzw. Hügel im Sand) beziehungsweise Dünen. Das Prinzip ist einfach und beruht auf den Gesetzen der Physik. Die Oberfläche des Sandes als solche ist instabil und so bereits durch schwache Umwelteinflüsse leicht zu verändern. Wenn also zum Beispiel ein leichter Wind in der Wüste oder eine sanfte Welle unter Wasser auf kommt, so verändert sich die gesamte Struktur des Sandes, wobei ein Sandkorn, das im Windschatten einer Muschel oder etwas vergleichbarem liegt, weniger stark bewegt wird als ein frei herumliegendes. Dies ist ein Beispiel der nicht zufälligen, wenn auch relativ willkürlichen Musterbildung. Eine zufällige Musterbildung wäre beispielsweise die der Fraktrale.

Der Goldener Schnitt

Der Golden Schnitt ist im wesentlichen nicht schwer zu verstehen. Teilt man eine Strecke, AB, am Punkt C, so dass die größere Strecke AC dividiert durch die Strecke BC dasselbe ergibt wie AC addiert mit BC und dann dividiert durch AC, steht die Strecke AC zur Strecke BC im Verhältnis des Goldenen Schnittes

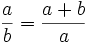
Dies gilt sowohl für Größen als auch für Zahlen. In der Natur ist der Goldene Schnitt z.B. Blattrosetten behilflich. Die aufeinanderfolgenden Blätter sind genau im "Golden Winkel" angeordnet. Der "Golden Winkel" wiederum ist der Winkel, der entsteht wenn man einen Kreis im Verhältnis des Goldenen Schnitts teilt. Nämlich ca. 137,5° zu 222,5°, wobei 137,5° der berühmt berüchtigter Winkel Psi ist.

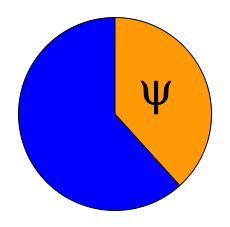
Und genau in diesem Winkel 137,5°, auch Psi genannt, wachsen bei vielen Pflanzen das eine Blatt zu nächsten!


Auf dieser Grafik kann man gut sehen das die Blatt 1 im Winkel Psi zu Blatt 2 steht. Doch welche Vorteile bringt diese Anordnung der Blätter?
Wenn die Blätter nun z.B. im Winkel 120° zu einander stehen würden, so würde jedes Blatt einanders Blatt für Sonnenlicht abdecken. So würde Blatt 1 von Blatt 4 verdeckt; Blatt 2 von Blatt 5; Blatt 3 von Blatt 6; und Blatt 4 wiederum von Blatt 7; usw. Dies wäre eine sehr schlechte Bedingung für die, in den Blättern stattfindende, Photosynthese, bei der sehr viel Sonnenlicht benötigt wird und für die Pflanze überlebenswichtig ist. Weil die aufeinanderfolgenden Blätter, wie in der Abbildung, im 137,5° Winkel angeordnet sind und so nur möglist wenig von den Blättern die unter sich liegen verdecken.

Die Fibonacci-Folge

"Lilien haben drei Blütenblätter, Butterblumen fünf, Ringelblumen 13, Astern 21 und die meisten Gänseblümchen 34, 55 oder 89. Andere Zahlen findest du nur selten,[…]".
(Quelle: http://math-www.uni-aderborn.de/~mathkit/Inhalte/Folgen/data/manifest28/Sonnenblume.html)
Dies schrieb Ian Stewart in einem Artikel für "Spektrum der Wissenschaft" und spielt damit auf die Bedeutung der Fiboncci-Zahlen in der Natur an.

Das f(n) steht für diejenige unbekannte Zahl, die an n-ter Stelle in der Fibonacci Folge.
Das f(n-1) steht demnach für eine Zahl, die eine Stelle vor f(n) steht.
So ist f(n-2) die Zahl, die zwei Stellen vor f(n) steht.
Um diese Formel besser zu verstehen, wenden wir sie doch gleich mal an:
Wir wollen auf die Zahl in der Fibonacci-Folge kommen, die an 8. Stelle steht.
Also f(8):

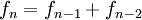
n = 8
f (n) = f (n-1) + f (n-2)

f (8) = f (8-1) + f (8-2)
f (8) = f (7) + f (6)
f (8) = 13+8

Doch um nochmal auf das Zitat einzugehen. Ian Stewart geht in seinem Artikel auf die Zusammenhänge der Fibonacci-Folge mit der Natur ein. Er nennt als Beispiel verschiedene Blumen und ihre Anzahl von Blütenblättern. Doch wir wollen ersteinmal ein anderes Beispiel bringen. Nämlich das von der Anordnung der Samenreifen einer Sonnenblume.

Dieses Bild stellt Aufbau von Samenreihen dar, wobei man bei genauem Hinsehen die Spiralen erkennt, die entweder rechts- oder linksrum laufen.

Man sieht sehr gut, dass die Samenreifen in Spiralen aufgebaut sind. Wenn man jetzt die Anzahl der rechtsdrehenden und die Anzahl der linksdrehenden Spiralen zählt:

Bei diesem Bild ist jetzt die Anzahl rechts- bzw. der linksdrehenden Spiralen gekennzeichnet.

So kommt man bei den rechtsdrehenden auf 34; und bei den linksdrehnden auf 55.
Oh Wunder 2 Zahlen in der Fibonacci-Folge aufeinander folgende Zahlen.
…; 21; 34; 55; 89;…

Warum das so ist, liegt auf der Hand:
Mit diesem "Code" kann die höchst mögliche Zahl an Samen auf kleinstem Platz untergebracht werden.

Entstehung komplexer Punktmuster

Dank dem Briten Alan Turing können wir diese Vorgänge erklären. Dieser hochintelligente Mensch und begnadete Mathematiker, der unter anderem den Verschlüsselungscode der Enigma knackte, erfand im Jahre 1952 eine Maschine, von der er behauptete, dass sie jedes mathematische Problem lösen könne, solange es auf einem Algorithmus beruhe. Durch die Erfindung dieses beinahe Computers machte die Mathematik bedeutende Fortschritte und kam unter anderem zu folgender Erkenntnis, welche die Musterbildung betrifft: Es gibt Stoffe die über weitere Entfernungen wirkten, die sogenannten Aktivatoren, sowie ihre eigene Entwicklung (was man Autokalyse nennt) und die ihres Pendants, der Inhibitoren, fördern. Diese Verbindung ist jedoch stark instabil. Wenn man mehr Aktivatoren hinzufügt, wächst auch die Menge der Inhibitoren an. Generell gilt, das sich der Inhibitor schneller ausbreitet, sodass er sich schnell vom Aktivator entfernt. Dadurch kann der Inhibitor die Autokalyse des Aktivators nicht aufhalten, sie allerdings auf die nähere Umgebung des Aktivators begrenzen. Es entsteht ein Hof um den Aktivator, der später als Punkt sichtbar wird. Auf diese Weise entstehen Punktmuster.

Was sind Muster?
Warum gibt es Muster?
Wie entstehen Muster im Sand?
Der Goldene Schnitt
Die Fibonacci-Folge
Entstehung komplexer Punktmuster
Nach oben